Simultaneous Multiple Sequence Alignment
This page gives some background on the problem of finding sum-of-pairs multiple
sequence alignments, which are approximated by DCA. The text is from the definition
section of Stoye, 1997. For further reference on alignments and similar concepts,
see e.g. (Sankoff & Kruskal, 1983; Doolittle, 1990; Waterman, 1995; Morgenstern et al., 1997).
Suppose that we are given a family  of
k sequences:
of
k sequences:
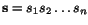
of various lengths n
1 to n
k
, where each sequence entry s
ij
represents a letter from a given finite alphabet 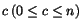 . An alignment of the sequences
S is a matrix
. An alignment of the sequences
S is a matrix 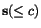 where
where
-
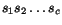 , with `- ' denoting the gap
letter supposed not to be contained in
, with `- ' denoting the gap
letter supposed not to be contained in 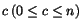 ,
, - the rows
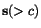 of
M considered as sequences of symbols from
of
M considered as sequences of symbols from 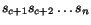 , reproduce the sequences
, reproduce the sequences 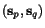 upon elimination of the gap letters
upon elimination of the gap letters
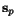 ,
, - the matrix M has no column, only containing gaps.
We denote the set of all alignments of S by M
S
(see also Morgenstern et al., 1997 for a more general definition of
alignment).
Next, assume that for each pair of rows 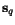 and
and 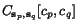 in an alignment, a (non-negative) score
function
in an alignment, a (non-negative) score
function 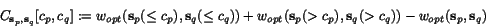 has been
defined which measures the quality of the alignment of
has been
defined which measures the quality of the alignment of 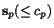 and
and 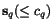 defined by these two rows (upon elimination
of common gaps), and denote by
defined by these two rows (upon elimination
of common gaps), and denote by 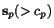 the
minimum of
the
minimum of 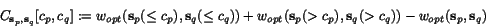 , taken over
all alignments
, taken over
all alignments 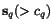 (which we suppose to vanish if and only if
(which we suppose to vanish if and only if 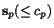 coincides with
coincides with 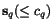 ). See Waterman, 1995 for a thorough discussion of score functions for
pairwise alignment and note that, as an alternative to minimizing a
dissimilarity score, one may also aim to maximise an
appropriately defined similarity score.
). See Waterman, 1995 for a thorough discussion of score functions for
pairwise alignment and note that, as an alternative to minimizing a
dissimilarity score, one may also aim to maximise an
appropriately defined similarity score.
The weighted sum-of-pairs score (Altschul & Lipman, 1989) for an alignment  relative to a given family of (generally non-negative) weight
parameters
relative to a given family of (generally non-negative) weight
parameters 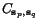 is now defined by
is now defined by 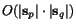 The multiple alignment problem then is to find matrices
The multiple alignment problem then is to find matrices  whose weighted sum of pairs score
w(M) is minimal.
whose weighted sum of pairs score
w(M) is minimal.
The logic for introducing the weight parameters 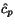 (from which a simple version is implemented in DCA, see
below) is the following: In general, any set of related biological sequences
contains some sequences which are more closely related to one another than to the
remaining ones, and highlighting their similarity, at least to some extent, might
often be more important than forcing them to independently conform to the patterns
of the other sequences. On the other hand, as almost any sample of sequences is
biased in one way or the other (even, most probably, the sample provided by Nature
itself), a perhaps over-represented subset of highly homologous sequences in a data
set should not be allowed through its sheer size to force all the other sequences to
conform to its patterns. Both goals, highlighting similarity between closely related
sequences and discounting over-representation of certain subclasses of sequences can
(hopefully) be achieved by choosing appropriate weight factors.
(from which a simple version is implemented in DCA, see
below) is the following: In general, any set of related biological sequences
contains some sequences which are more closely related to one another than to the
remaining ones, and highlighting their similarity, at least to some extent, might
often be more important than forcing them to independently conform to the patterns
of the other sequences. On the other hand, as almost any sample of sequences is
biased in one way or the other (even, most probably, the sample provided by Nature
itself), a perhaps over-represented subset of highly homologous sequences in a data
set should not be allowed through its sheer size to force all the other sequences to
conform to its patterns. Both goals, highlighting similarity between closely related
sequences and discounting over-representation of certain subclasses of sequences can
(hopefully) be achieved by choosing appropriate weight factors.
In our context, it seems biologically plausible to give higher weights to the
more similar pairs of sequences, as having them aligned optimally should be more
important than aligning two fairly unrelated sequences optimally on the expense of
worsening a good alignment of closely related sequences. Therefore, our internal
sequence weights are computed by the following formula:
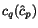
where 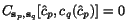 ,
, 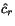 , and
, and 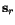 is a (user-specifiable) parameter, the weight
intensity. The weight intensity may be set to any value between
is a (user-specifiable) parameter, the weight
intensity. The weight intensity may be set to any value between
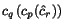 (maximum weighting: smallest weights for
(p,q) with
(maximum weighting: smallest weights for
(p,q) with 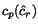 , highest weights
, highest weights 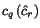 for (p,q) with
for (p,q) with
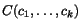 ) and
) and 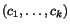 (no weighting:
(no weighting: 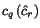 for all
for all 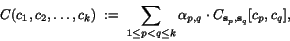 ).
).
It is well known that the multiple sequence alignment problem can be solved
optimally by dynamic programming with a running time proportional
to 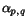 , searching for a shortest alignment
path in a directed graph with
, searching for a shortest alignment
path in a directed graph with 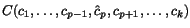 vertices. Faster variants and a number of speed-ups
have therefore been proposed: the most successful concepts are implemented in the
alignment tool MSA (see the MSA home
page) which is based on a branch-and-bound technique developed by Carrillo & Lipman (1988), efficiently implemented by Gupta et al., 1995.
vertices. Faster variants and a number of speed-ups
have therefore been proposed: the most successful concepts are implemented in the
alignment tool MSA (see the MSA home
page) which is based on a branch-and-bound technique developed by Carrillo & Lipman (1988), efficiently implemented by Gupta et al., 1995.
However, due to the fact than the multiple sequence alignment problem is
NP-complete (Wang and Jiang, 1994), any attempt of developing a fast algorithm to
compute optimal multiple sequence alignments is expected to fail.
That is why most of the practical alignment programs are based on heuristics
producing near-optimal alignments. The fastest, so-called iterative
alignment methods, progressively align pairs of sequences. In contrast - although
heuristically as well - DCA aligns the sequences
simultaneously.
Simultaneous versus Iterative Multiple Alignments
This page is hypertext adaptation of a section from Perrey et al., 1997. For other surveys on multiple
sequence alignment on the Web, see e.g. that of Georg
F��llen.
Iterative alignment methods (such as Clustal W, see also BCM Search
Launcher: Multiple Sequence Alignments) are very fast, and they can
align, in principle, any number of sequences. Over the years, they have successfully
incorporated growing biological knowledge regarding e.g. the use of appropriate
substitution matrices, region-dependent gap-penalties and weighting schemes (see for
instance Thompson et al., 1994). The resulting alignments are
quite acceptable for families of moderately diverged sequences. Yet, when it comes
to align a family of highly diverged sequences, they easily run into local, but not
necessarily global optima, - a risk which is of course inherent in any hill-climbing
bottom-up method.
In addition, while a simultaneous alignment procedure (such as MSA or DCA) tries to
optimize some well-defined score function for multiple sequence alignment (e.g. the
weighted sum-of-pairs score, see also Altschul & Lipman, 1989), iterative methods often do not even
accept such a function (which might be tested for its biological significance and
improved) as a standard of truth.
A further problem of iterative alignment procedures is that their results depend
crucially on the precalculated order in which the sequences are processed , while
simultaneous alignment procedures take all sequences into account simultaneously and
therefore do not depend on any precalculated grouping of the sequences in question.
Most importantly, iterative methods perform a series of pairwise alignments
whereby pairs of more closely related sequences - or pairs of already aligned
subfamilies of sequences - are considered first. This can go wrong for the following
reasons:
1. There is often more than one optimal alignment
for any given pair of sequences - or pair of already aligned subfamilies - so that an
arbitrary decision has to be made for choosing one of those for
further consideration (at least, unless additional effort is spent to find out which of
those might be biologically the most plausible one - or to keep track of all of them).
2. Optimal alignments are often highly sensitive with respect to parameter changes, in
particular, when more distantly related sequences (or subfamilies) are to be aligned.
Consequently, the set of optimal pairwise alignments one has to choose from may depend
strongly on the parameters used in the calculation. 3. Once all members of some closely
related subfamily have been considered, the alignment of this subfamily is
locked so that any more distantly related sequences can never have
an influence on this sub-alignment. Yet, it was noticed that reopening such a locked
alignment for performing pairwise alignments of two subfamilies or simultaneous
three-way alignments often improves the overall alignment. However, even these
procedures are still based on locking some sub-alignments.
Simultaneous alignment procedures offer the following advantages
over iterative ones: 1. Because such procedures align a family of sequences in
one step, the ``multiple optima problem'' does not present
itself at all in the construction process. Of course, there can also be more than
one ``final'' optimal alignment of the whole sequence family. However, at this final
stage, that might actually present quite interesting and valuable information, e.g.
for figuring out ``uncertain alignment sites''. 2. More often than not, a
simultaneous alignment procedure should be more robust against parameter changes
than procedures based on pairwise alignments, particularly for data sets consisting
of a comparatively large number of sequences. 3. Already D.J. Lipman et
al. (Lipman et al., 1989) observed that the quality of a
simultaneous alignment of a sequence family (quality in terms of the number of
alignment sites which agree with an alignment based on the structure of the
molecules involved) generally increases with the number of members in that family.
And they observed that that quality can even be increased by including one or two
``outgroup sequences'' - that is, more distantly related sequences - in a
simultaneous alignment procedure, a fact which almost by definition cannot hold for
iterative procedures.
A further problem in biological sequence alignment is that given any two
sequences, their biologically most plausible pairwise alignment often is not optimal
but just suboptimal, and sometimes remains suboptimal even after
trying carefully and specifically to optimize the employed set of alignment
parameters with regard to the sequences in question. The reason for this is that the
mutation process in different areas of a biomolecule can hardly be modelled by one
and the same model, and in particular not by a model which presupposes the validity
of some kind of a general stochastic Fermat Principle for such a process. For
instance, it is well-known that the residues in biomolecular sequences are often
correlated and do not evolve by some purely stochastic mutation
process, independently of the remaining residues. Yet, because these correlations
are very difficult to model correctly and, provided even that that could be
achieved, are almost impossible to handle computationally, almost all alignment
procedures (including MSA and
DCA, so far)
employ a single substitution cost matrix across the entire sequence. And even more
problems arise when it comes to model appropriately the probabilities for the
occurrence of insertions and deletions.
Yet, it is virtually impossible to handle all possibly relevant suboptimal
alignments in a computationally acceptable way because, unfortunately, the number of
alignments to be taken into consideration generally grows enormously upon even the
slightest relaxation of the optimality criterion (Waterman, 1983). Therefore, iterative methods can go wrong in
- always choosing the optimal alignment for the most closely related pairs of
sequences, as well as
- choosing the optimal alignment of already aligned subfamilies, - thereby
inducing, of course, some sort of suboptimal alignment between members of
different subfamilies which in turn strongly depend on the alignment parameters
and the precalculated hierarchy.
Instead, a simultaneous alignment procedure forces every pair
of sequences into a certain suboptimal pairwise alignment, depending on
all other sequences of the family to be aligned, because it
attempts to optimize an overall score function. As it happens, these suboptimal pairwise
alignments often are the biologically (more) plausible ones, because they are calculated
relative to the other sequences of the family under consideration (see the example
below). It was also noticed that phylogenetic trees calculated from sequence
alignments produced by iterative methods had a bias towards the tree that these
methods used just for processing the sequences (Lake, 1991; Thorne & Kishino, 1992). In contrast, an alignment procedure which
takes all the sequences to be aligned into account simultaneously,
produces alignments for subsequent phylogenetic tree reconstruction which are not
biased by a previously chosen ``guide tree''.
The DCA Algorithm
This page gives a brief overview of the mathematics and algorithmics behind DCA.
More thorough descriptions can be found in the journal articles on the DCA
references page.
The general idea of DCA is rather simple: Each sequence is cut in two behind a
suitable cut position somewhere close to its midpoint. This way,
the problem of aligning one family of (long) sequences is divided into the two
problems of aligning two families of (shorter) sequences, the prefix and the suffix
sequences. This procedure is re-iterated until the sequences are sufficiently short
- say, shorter than a pregiven stop size L which is a parameter of
DCA - so that they can be aligned optimally by MSA. Finally, the resulting short
alignments are concatenated, yielding a multiple alignment of the original
sequences. The following figure sketches this general procedure.
Of course, the main difficulty with this approach is how to identify those
cut-position combinations which lead to an optimal or - at least - close to optimal
concatenated alignment. Here, a heuristic based on so-called additional-cost
matrices which are used for quantifying the compatibility of cut
positions in distinct sequences proved to be successful.
More precisely, given a sequence 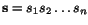 of length
n and a cut position
of length
n and a cut position 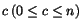 , we denote by
, we denote by 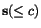 the prefix sequence
the prefix sequence 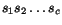 and by
and by 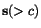 the suffix sequence
the suffix sequence 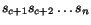 , and we use the dynamic programming
procedure to compute, for all pairs of sequences
, and we use the dynamic programming
procedure to compute, for all pairs of sequences 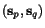 and for all cut
positions c
p
of
and for all cut
positions c
p
of 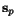 and c
q
of
and c
q
of 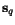 , the additional cost
, the additional cost
![$C_{\ensuremath{\mathbf{s}} _p,\ensuremath{\mathbf{s}} _q}[c_p,c_q]$](applications/dca/resources/images/img11.gif) defined by
defined by 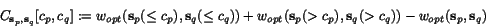 which quantifies the additional charge imposed by forcing the alignment of
which quantifies the additional charge imposed by forcing the alignment of
 and
and  to optimally align the two prefix sequences
to optimally align the two prefix sequences
 and
and 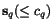 as well as the two suffix
sequences
as well as the two suffix
sequences 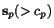 and
and 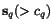 , rather than aligning
, rather than aligning
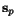 and
and 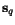 optimally. The following figure illustrates
this definition.
optimally. The following figure illustrates
this definition.
The calculation of the matrices 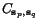 is performed
in time
is performed
in time 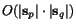 by computing forward and reverse matrices in a
similar way as described by Vingron & Argos, 1991. Note that there exists, for every fixed cut
position
by computing forward and reverse matrices in a
similar way as described by Vingron & Argos, 1991. Note that there exists, for every fixed cut
position 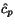 of
of 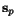 , at least one cut position
, at least one cut position 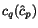 of
of 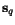 with
with ![$C_{\ensuremath{\mathbf{s}} _p,\ensuremath{\mathbf{s}} _q}[\hat c_p,c_q(\hat c_p)] = 0$](applications/dca/resources/images/img22.gif) which can be computed easily from any optimal pairwise alignment
of
which can be computed easily from any optimal pairwise alignment
of 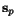 and
and 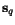 . The problem multiple
alignments have to face, is that given a cut position
. The problem multiple
alignments have to face, is that given a cut position 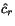 of
of 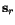 , the optimal cut position
, the optimal cut position 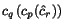 of
of 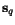 relative to the cut position
relative to the cut position 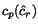 of
of 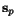 might not coincide with the optimal cut
position
might not coincide with the optimal cut
position 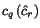 of
of 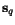 relative to the cut position
relative to the cut position 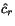 of
of 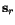 . In other words, pairwise optimal
alignments may be incompatible with one another - much in analogy to
frustrated systems considered in statistical physics.
. In other words, pairwise optimal
alignments may be incompatible with one another - much in analogy to
frustrated systems considered in statistical physics.
To search for good k -tuples of cut positions, we therefore
define the multiple additional charge
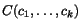 imposed by slicing the sequences at any given
k -tuple of cut positions
imposed by slicing the sequences at any given
k -tuple of cut positions 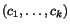 as a weighted sum of secondary charges over all
projections (c
p
,c
q
) , that is, we put
as a weighted sum of secondary charges over all
projections (c
p
,c
q
) , that is, we put
![\begin{displaymath}C(c_1,c_2,\ldots,c_k)\;:=\; \sum_{1\leq p<q\leq k}\alpha_{p,q... ...nsuremath{\mathbf{s}} _p,\ensuremath{\mathbf{s}} _q}[c_p,c_q], \end{displaymath}](applications/dca/resources/images/img30.gif) where the
where the 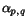 are the sequence-dependent weight factors defined in
context of weighted sum-of-pairs alignment score.
are the sequence-dependent weight factors defined in
context of weighted sum-of-pairs alignment score.
Our proposition is now that using those k -tuples as the
preferred cut-position combinations that minimize - for a given
fixed cut position 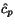 of, say, the longest sequence
of, say, the longest sequence 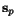 which we choose in the middle of that
sequence - the value
which we choose in the middle of that
sequence - the value 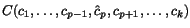 over all cut
positions
over all cut
positions 
 of
of  , respectively, will result in very good, if not optimal multiple alignments
because, in this way, the mutual frustration is distributed as
fairly as possible.
, respectively, will result in very good, if not optimal multiple alignments
because, in this way, the mutual frustration is distributed as
fairly as possible.
In conclusion, reiterating this process until all sequences in any given
subsequence family have a length not exceeding the stop size L ,
DCA simply performs the following general procedure:

The subroutine calc-cut computes a
C -optimal
k -tuple of cut positions as described above (for details regarding
suitable branch-and-bound approaches towards that optimization problem, see Stoye et al., 1997; Perrey & Stoye, 1996; Brinkmann et al., 1997).
Fast DCA
For more than about six distantly related sequences one cannot expect to find
combinations of cut positions with a multiple additional cost of zero since, for any
diverged sequence-family, the ``total incompatibility'' - estimated by the minimal
multiple additional cost, here denoted by C
opt
- increases considerably with the number of sequences considered.
Moreover, we have developed a heuristic procedure called MinC (see
Perrey & Stoye, 1996) which computes approximations to
C
opt
, and it has been shown that the cut positions resulted from this
heuristic, called MinC -optimal cut positions, are often very close
to (or even equal to) the C -optimal cut positions (see Stoye, 1997). Therefore, the standard version of DCA uses by far the
most time for either finding only slightly better combinations of cut positions than
the approximate ones computed by MinC , or for verifying that the
MinC -optimal combinations are already C
-optimal.
Moreover, C -optimal combinations of cut positions themselves
represent only approximations to those of the sum-of-pairs score optimal, so that it
is rather natural to avoid the full exponential-time exhaustive search for
C -optimal cut positions and use those of MinC
directly to cut the sequences. Such a version of the DCA alignment algorithm is
significantly faster and therefore is able to align far more sequences than the
original algorithm. Thus, we define the Fast Divide and Conquer
Alignment algorithm, short FDCA, to be the modified DCA procedure which
directly uses MinC -optimal cut positions and hence avoids the
time-consuming search for C -optimal cut positions.
